Neste resumo de Funções 10º Ano, aprende tudo scom a melhor compilação de vídeos, resumos e exercícios!
Até vais aprender como tu próprio podes explorar a matéria! 🤩
🗂️Índice
- Todos os recursos deste artigo
- Pré-requisitos
- O que é uma função ⭐⭐⭐
- Propriedades
- Zeros e Sinal ⭐⭐⭐
- Extremos ⭐⭐⭐
- Monotonia ⭐⭐⭐
- Paridade ⭐⭐
- Função Injetiva, Sobrejetiva, Bijetiva⭐
- Funções clássicas
- Função constante ⭐⭐⭐
- Função afim ⭐⭐⭐
- Função quadrática
- Função módulo
- Novas funções a partir das velhas
- Restrições
- Função definida por ramos
- Transformações de funções
- Função inversa
- Função composta
- Em breve…
Significado das estrelas:
⭐⭐⭐ : Muito importante (essencial para agora e aprendizagens futuras, muito comum em exame)
⭐⭐: Algo importante (essencial principalmente para agora, mais raro em exame)
⭐: Menos importante (não sai em exame, mas alguns professores podem abordar)
📂Todos os Recursos deste artigo
| Todos os vídeos (playlist do YouTube) |
| Todos os exercícios (pasta do Google Drive) |
📝Pré-requisitos
Para perceberes esta aula toda, tens de saber:
✅Operar com números reais (incluindo frações, potências e raízes)
✅Resolver equações e inequações
(revê as equações e inequações no vídeo abaixo)
🌱O que é uma função?
Vê o vídeo para perceberes os básicos sobre funções:
De facto, há várias maneiras de representar uma função:
1. diagrama de setas
2. tabela
3. expressão analítica
4. gráfico
Porém, na prática, a expressão analítica e o gráfico serão usados 99% das vezes daqui para a frente (só agora para começar é que vais ver um pouco mais de diagramas de setas e tabelas).
Outra perspetiva
Pessoalmente, gosto de pensar numa função como o deslocar de pontos de uma posição inicial para uma posição final.
Aos pontos na posição inicial chamamos objetos e à posição final desses pontos chamamos imagens.
Ou se quisermos falar nestes pontos como um todo: ao conjunto de todos os pontos na posição inicial chamamos de domínio e a todos as posições finais desses pontos chamamos de contradomínio. Além disso, o conjunto de todas as possíveis posições finais chamamos de conjunto de chegada
No fundo, o domínio são os nossos pontos, o contradomínio é para onde eles vão e o conjunto de chegada é para onde eles poderiam ir. Ou dizendo ainda melhor:
O domínio é o “antes” e o contradomínio é o “depois”.
PS: E o conjunto de chegada só importa nestes exercícios iniciais e depois podes esquecê-lo para sempre até entrares na Universidade 😜
Ao imaginares as funções como uma deslocação de pontos, então torna-se óbvio o que é e não é função: é óbvio que um ponto não se pode deslocar para dois sítios diferentes e é também óbvio que não pode desaparecer – tem sempre de ir para algum lado.
Depois, a expressão analítica de uma função é apenas uma fórmula que te diz para onde deslocar cada ponto. No fundo, diz-te como obter o “depois” sabendo o “antes” (mas também te diz como obter o “antes” sabendo o “depois”!). No fundo:
Uma expressão analítica é uma “ponte” que liga o x ao f(x). Se souberes um, sabes o outro (e vice-versa)!
Exercícios: fichas de trabalho
Só com isto que acabaste de ver, já deves ser capaz de:
🔴 saber o que é e não é uma função
🔴 identificar o domínio, contradomínio e conjunto de chegada de uma função
🟡 determinar a imagem f(x), sabendo o objeto x
🟡 determinar o objeto x, sabendo a imagem f(x)
🟡 resolver condições envolvendo funções (por exemplo, f(x)>2)
🟢 esboçar o gráfico, sabendo a expressão analítica
🟢 escrever a expressão analítica, sabendo o gráfico
Mas nada melhor do que fazer exercícios: 😁
| Exercícios Básicos (exceto 5.3, 6.3, 7.4) Mentes Brilhantes (website) | Ficha (com Soluções) |
Exercícios: faz tu!
EXERCÍCIO 1: No plano, faz o desenho que te apetecer e pergunta-te se isso é o gráfico de uma função ou não.
EXERCÍCIO 2: No plano, desenha o gráfico de uma função que te apetecer e faz-te as cinco perguntas-chave:
🔴 identificar o domínio, contradomínio e conjunto de chegada de uma função
🟡 determinar a imagem f(x), sabendo um objeto x
🟡 determinar o objeto x, sabendo a imagem f(x)
🟡 resolver uma condição (por exemplo, f(x)>2)
🟢 escrever a expressão analítica dessa função, ou seja, f(x)=… (no caso de teres escolhido uma função muito simples)
EXERCÍCIO 3: Escreve a expressão analítica da tua função preferida. Agora, faz-te as mesmas perguntas que fizeste no exercício 2, só que a última questão agora é:
🟢 esboça o gráfico dessa função
🔬Propriedades das Funções (investigação gráfica)
Vamos imaginar que somos matemáticos e que acabámos de inventar as funções. Agora, a grande é: quais são as características interessantes de uma função?
Talvez seja mais fácil fazer a pergunta em termos de gráficos: quais são as características interessantes de um gráfico?
⛵Sinal e Zeros
Ora, uma das perguntas mais naturais é: para que valores de x é que o gráfico está acima, está abaixo ou interseta o eixo dos xx?
Ou, perguntando de outra maneira: para que valores de x é que a a função é positiva, negativa ou zero?
Ou, perguntando ainda de outra maneira: para que valores de x temos f(x)>0, f(x)<0 ou f(x)=0?
Responder a esta pergunta é aquilo a que se chama “estudar o sinal e os zeros de uma função“.
Vê o vídeo para perceber como estudar graficamente o sinal e os zeros (vê até aos 8:40):
Por vezes, em vez de darmos as nossas respostas apresentando o conjunto-solução, dá mais jeito resumir essa informação apresentando um quadro de sinal (ou tabela de sinal).
Descobre como fazer um quadro de sinal neste vídeo:
Exercícios: fichas de trabalho
Só olhando para o gráfico de uma função, já deves ser capaz de:
🔴 Dizer para que valores de x uma função é positiva, negativa ou zero (estudar o sinal e zeros)
🔴 Fazer o quadro de sinal
🟡 Resolver outras condições envolvendo funções
| Gráficos: zeros, sinal, resolução de condições Prof. Roberto Oliveira (website) | Ficha (com Soluções) |
Exercícios: faz tu!
EXERCÍCIO 1: Desenha o gráfico das funções que te apetecerem e responde a todas as perguntas-chave:
🔴Diz o Domínio e o Contradomínio da função
🔴 Estuda o Sinal e Zeros da função (primeiro, escreve o conjunto-solução de cada condição f(x)=0, f(x)>0 e f(x)<0 e depois resume tudo num quadro de sinal)
🔴 Apresenta o conjunto-solução de outras condições que te apetecerem (por exemplo, f(x)=-2, f(x)≤1 ou f(x)+f(2)-f(1)>4)
EXERCÍCIO 2: Desenha um quadro de sinal que te apeteça. Depois, esboça o gráfico de uma função que tenha esse quadro de sinal.
🏔️Extremos relativos e extremos absolutos
Extremos Absolutos
Depois, há outra pergunta, talvez ainda mais natural para perguntar sobre um gráfico: qual é o “pico mais alto e o “vale” mais baixo do nosso gráfico?
Ou, perguntando de outra maneira, qual é o valor mais alto e mais baixo da nossa função?
Ou, em linguagem matemática, qual é o máximo absoluto e o mínimo absoluto da nossa função?
Certamente percebeste: máximo porque é o valor mais alto, mínimo porque é o valor mais baixo. Mas porquê “absoluto?” É absoluto porque é o valor mais alto ou mais baixo de toda a função.
Matematicamente, dizemos que o valor da função f(c) é máximo absoluto se for maior ou igual a todos os valores da função:
f(c) é Máximo Absoluto:
f(c) ≥ f(x)
(para todos os x no domínio de f)
Do mesmo modo, dizemos que o valor da função f(c) é mínimo absoluto se for menor ou igual a todos os valores da função:
f(c) é Mínimo Absoluto:
f(c) ≤ f(x)
(para todos os x no domínio de f)
🔴ATENÇÃO: Os máximos e mínimos são valores de y!
Quando não queremos especificar se é mínimo absoluto ou máximo absoluto, apenas dizemos extremo absoluto.
Ou seja, um extremo absoluto pode ser tanto um máximo absoluto ou um mínimo absoluto.
Revê a definição e vê um exemplo neste vídeo:
Extremos (Relativos)
Mas claro, num gráfico, não é só o “pico” mais alto e o “vale” mais baixo que são interessantes!!!
De facto, nós gostamos de todos os picos e todos os vales! 😋
Ou seja, nós gostamos de todos os máximos relativos e de todos os mínimos relativos.
E porquê “relativos”? São relativos porque são o maior ou menor valor numa pequena região (de x) à volta desse ponto.
🔴ATENÇÃO: Os máximos e mínimos absolutos também são máximos e mínimos relativos (porque se são os maiores ou menores valores de toda a função, então certamente são os maiores/menores valores numa pequena região de x à volta desse ponto)
Por esta razão, em vez de dizermos máximos relativos e mínimos relativos, apenas dizemos máximo e mínimos (porque já sabemos que inclui todos os “picos” e “vales”, sejam eles os maiores de todos ou não).
E tal como dantes, aos máximos e mínimos (relativos) chamamos de extremos (relativos).
Vê estes dois exemplos – vais perceber melhor: 😁
Maximizantes e Minimizantes
Não sei se já viste, mas para reforçar: 😏
🔴ATENÇÃO: Os máximos e mínimos são valores de y!!!
Aos respetivos valores de x, chamamos de maximizante e minimizante. Ou seja:
Maximizante: valor de x para o qual temos um máximo.
Minimizante: valor de x para o qual temos um mínimo.
Pormenores importantes (e exercício em vídeo)
Só olhando para o gráfico de uma função, já deves ser capaz de:
🔴 Indicar todos os extremos (relativos)
🔴 Indicar os extremos que são absolutos
🔴 Indicar os respetivos maximizantes e minimizantes
Pausa o vídeo e indica os extremos absolutos e os extremos relativos da função (se existirem). Depois vê a resolução:
🔴ATENÇÃO: Se a função é constante algures, então em todos esses pontos temos extremos relativos.
🔴ATENÇÃO: Repara que os extremos absolutos têm de ser valores da função. Por isso, às vezes os extremos absolutos não existem (quando o valor mais alto ou baixo não pertence à função, por exemplo, no caso de ter bola aberta).
Exercícios: faz tu!
EXERCÍCIO 1: Desenha o gráfico das funções que te apetecerem e indica (se existirem):
🔴 os extremos relativos e absolutos
🔴 os respetivos minimizantes e maximizantes
📈Monotonia
Há outra pergunta extremamente natural que podemos fazer sobre um gráfico: para que valores de x é que a função cresce, decresce ou não muda?
Ou, em linguagem matemática, para que valores de x é que esta função é crescente, decrescente ou constante?
E agora, é só traduzir para definições matemáticas.
Função constante, é óbvio:
f constante no intervalo [a,b]:
f(x1)= f(x2),
para todos os valores x1, x2 nesse intervalo [a,b]
Se a função for sempre constante, ou seja, constante em todo o seu domínio, então dizemos que é uma função constante. (óbvio! 😜)
Vê as definições de crescente, decrescente e monótona no vídeo (vê até aos 20.22):
No fundo:
🟡 Crescente em sentido lato = Estritamente Crescente ou Constante
🟡Decrescente em sentido lato = Estritamente Decrescente ou Constante
🟡 Monótona = sempre estritamente crescente ou sempre estritamente decrescente
🟡Não monótona = não é monótona
🟡Monótona em sentido lato = sempre estritamente crescente/constante ou sempre estritamente decrescente/constante
🔴ATENÇÃO: Há autores que chamam crescente à função estritamente crescente e há outros que chamam crescente à função crescente em sentido lato
(a definição que dei é a que está no Programa e Metas, mas, na dúvida, fala com o teu professor)
Aqui, a pergunta clássica é “faz o quadro/tabela de variação e indica os intervalos de monotonia“
Aqui, o quadro de variação é como o quadro de sinal (só que agora em vez de teres + ou –, tens ↘,↗ ou →)
Vê um exemplo rápido de como construir o quadro:
E agora vê um exemplo mais completo, em que não só fazes a tabela mas também escreves os intervalos de monotonia (vê até aos 6:30):
🔴ATENÇÃO: Quando escreves os intervalos de monotonia, não interessa se metes intervalo aberto ],[ ou fechado [,] (pessoalmente eu gosto mais de fechado, mas, na dúvida, pergunta ao teu professor)
Mas cuidado: se o ponto não estiver no domínio, então terá obrigatoriamente de ser intervalo aberto! (isto tu já sabias)
Exercícios: Fichas de Trabalho
Só olhando para o gráfico de uma função, já deves ser capaz de:
🔴 Indicar os intervalos de monotonia
🔴 Fazer o quadro/tabela de variação
🟡 Justificar se uma função é ou não é monótona
| Monotonia (não fazer: 1 e 5) Mentes Brilhantes (website) | Ficha (com Soluções) |
Exercícios: faz tu!
EXERCÍCIO 1: Desenha o gráfico das funções que te apetecerem. Depois, faz o seu quadro de variação e indica os intervalos de monotonia.
EXERCÍCIO 2: Desenha um quadro de variação que te apeteça. Depois, esboça o gráfico de uma função que tenha esse quadro de variação.
EXERCÍCIO 3: Desenha um quadro de sinal e um quadro de variação que te apeteça (só precisam de ter o mesmo domínio). Depois, esboça o gráfico de uma função que tenha esses quadros de sinal e de variação.
ATENÇÃO: é possível que tal função não exista, por isso escolhe bem os teus quadros!
⛵Paridade
Se estivermos mesmo com sorte, então a nossa função pode ter alguma simetria.
Está tudo bem explicado neste vídeo (vê até aos 56:23):
Resumindo:
🟡Par: simétrica com eixo dos yy
f(-x)=f(x)
🟡 Ímpar: simétrica com a origem:
f(-x)=-f(x)
🟢Curiosidade: Se já sabes a composição de funções, as funções chamam-se pares e ímpares porque compor funções pares e ímpares é como multiplicar números pares e ímpares: par com par fica par, par com ímpar fica par, ímpar com ímpar fica ímpar!
Exercícios: fichas de trabalho
| Funções pares e ímpares Mentes Brilhantes (website) | Ficha (com Soluções) |
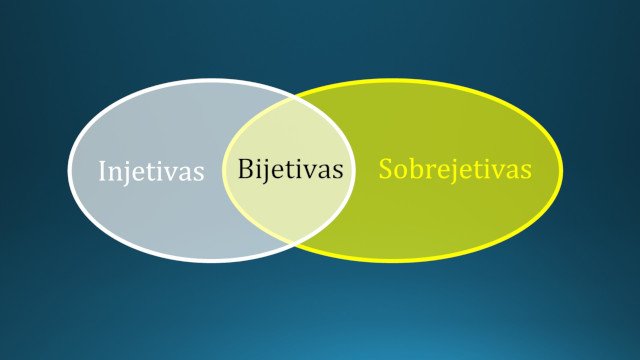
🧹Funções injetivas, sobrejetivas e bijetivas
Uma questão mais engenhosa que podemos perguntar é: quantas vezes é que a função toma cada valor de y?
Se pensares bem, esta pergunta só tem a ver com os yy, ou seja, com o contradomínio.
É com base na resposta a essa pergunta que definimos funções injetivas, sobrejetivas e bijetivas.
Está tudo bem explicado neste vídeo (vê até aos 17:11):
No fundo:
Exercícios: fichas de trabalho
| Funções injetivas, sobrejetivas e bijetivas Mentes Brilhantes (website) | Ficha (com Soluções) |
Exercícios: faz tu!
EXERCÍCIO 1: Desenha o gráfico da função que te apetecer e diz se é injetiva, sobrejetiva ou bijetiva.
DICA: “Lava a parede”, ou seja, olha ao longo do eixo dos yy
EXERCÍCIO 2: Desenha o gráfico de uma função:
2.1 – Bijetiva
2.2 – Injetiva mas não sobrejetiva
2.3 – Sobrejetiva mas não injetiva
ATENÇÃO: Tem de ser mesmo uma função!!! (ou seja, não te metas a desenhar linhas verticais ou outras coisa que tenham mais do que valor de y para cada valor de x).
🤩Em breve…
- Tudo o que está nas Aprendizagens Essenciais de 10º Ano (par e ímpar, transformações, quadrática, polinómios, função módulo e definidas por ramos)
- Tudo que está no Programa e Metas Curriculares de 10º Ano (composta, inversa, injetiva, sobrejetiva e bijetiva, funções racionais e irracionais)
- Até lá, espreita este resumo de funções 10º Ano:
🧐Funções clássicas
Função constante
A função constante é uma função do tipo f(x)=b, em que b é um número real qualquer.
Pensando em pontos, é aquela função em que todos os pontos se movem para o mesmo sítio, ou seja, todos o objetos movem-se para a mesma imagem.
Graficamente, isto é uma reta horizontal.
Função afim
Uma função afim é uma função do tipo f(x)=ax+b.
Graficamente, é a uma reta oblíqua (ou seja, uma reta “inclinada”).
No fundo, o gráfico é aquele em que começas em b (quando o x é 0) e de cada vez que o x aumenta 1 unidade, o y aumenta “a” unidades.
Exercícios: fichas de trabalho
| Função afim Mentes Brilhantes (website) | Ficha (com Soluções) |
🙋♂️🙋♀️Até lá, quero ouvir as tuas sugestões!
Tens alguma questão? Ou tens o recurso perfeito para adicionar a este resumo?
Conta-me tudo nos comentários! 😁⬇️

