Aprende passo a passo toda a matéria de Sucessões 11º Ano com a melhor compilação de vídeos, resumos e exercícios!
Até vais aprender a criar os teus próprios exercícios! 🤩
🗂️Índice
- Todos os recursos deste artigo
- Pré-requisitos
- Aprendizagens Essenciais
- O que é uma sucessão
- Sucessões definidas por recorrência
- Progressões Aritméticas e Geométricas
- Propriedades
- Limites de sucessões
- Relação entre convergência, monotonia e limitação
- Outras dicas e truques
- Fichas globais
- Exercícios de Exame
- Testes-modelo
- Preciso da tua ajuda!
📂Todos os Recursos deste artigo
| Todos os vídeos (playlist do YouTube) |
| Todos os exercícios (pasta do Google Drive) |
📝Pré-requisitos
Para perceberes esta aula toda, tens de saber:
✅Operar com números reais (incluindo frações, potências e raízes)
✅Resolver equações e sistemas de equações
✅Fazer divisão de polinómios
Revê equações e sistemas neste vídeo:
Revê rapidamente a divisão de polinómios neste vídeo (vê até aos 6:53):
✅Aprendizagens Essenciais
Oficialmente, tens de aprender os conteúdos que estão nas Aprendizagens Essenciais 11º Ano:

No fundo, tens de saber:
1. Progressões Aritméticas, Progressões Geométricas e Sucessões definidas por recorrência
2. Limites de sucessões
3. Sucessões convergentes, monótonas e limitadas
🌱O que é uma sucessão?
Uma sucessão é só uma maneira de colocar a ideia de sequência de números (por exemplo, 1,2,3,4,5,… ou 2,4,6,8,10,…) em linguagem matemática.
Podes descrever uma sucessão de 3 perspetivas:
1. como uma função que só aceita números naturais
2. pelo seu termo geral
3. pelo seu gráfico
Na prática, a primeira (que é a definição), é-nos inútil. As perspetivas importantes são o termo geral e o gráfico (que, se pensares bem, é como nas funções: gostamos da expressão geral e do gráfico 😉).
Mais info no vídeo:
Exercícios
Só com isto que acabaste de ver, já deves ser capaz de:
🔴 calcular o termo de ordem …
🔴 calcular a ordem do termo … (ou verificar se o termo pertence ou não pertence à sucessão)
🔴 calcular ordem dos termos que estão num determinado intervalo
🟡esboçar o gráfico, calculando os primeiros termos
🟢descobrir o termo geral [mais desafiante e não tão importante]
Aqui, para calcular ordens e termos, tens de estar muito confortável a resolver equações. Vê estes dois exercícios clássicos neste vídeo:
Agora é a tua vez! 😁🔥Começa e pausa o vídeo para resolveres o exercício. Quanto terminares, continua o vídeo para veres a resolução: (qualquer dúvida, vê o exemplo anterior)
E agora pratica ainda mais! Os exercícios de descobrir o termo geral são opcionais – fá-los como um desafio! 😉
Os exercícios de calcular ordens de termos num determinado intervalo é parecido com o de calcular a ordem de um termo, só que agora tens de resolver uma inequação.
| Descobrir termo geral, calcular ordens e termos (ex. 1, 2, 3 opcional) Mentes Brilhantes (website) | Ficha (com Soluções) |
| Calcular termo geral, termos, ordens e ordens num intervalo (ex.1, 6, 7, 8 opcionais) Prof. Lara Reis (website) | Ficha |
| Calcular termos num determinado intervalo (ex. 4 e 10) Prof. Paulo Correia (Exame) (website) | Ficha Resolução |
♻️Sucessões definidas por recorrência
Mas a maneira mais natural de nós inventarmos sucessões de números não é com um termo geral, mas sim começando com um primeiro termo e depois, sabendo como obter o termo seguinte a partir do anterior.
Por exemplo, imagina a sucessão 1,2,3,4,5,…
A primeira coisa que te vem à cabeça nunca é “ora, esta é a sucessão de termo geral n“. 😏
Aquilo que te vai à cabeça é: “esta é a sucessão em que começamos no 1 e para obter o termo seguinte a partir do anterior somamos 1“
Ora, às sucessões definidas desta segunda maneira, mais natural, chamamos sucessões definidas por recorrência (recorrência, porque para criar a sucessão toda a partir do primeiro termo, seguimos um processo que é repetitivo, recorrente, ou seja, uma recorrência).
Exercícios
Vê este vídeo, para perceberes melhor como calcular os termos seguintes a partir do primeiro:
Só com isto que acabaste de ver, já deves ser capaz de:
🔴calcular os primeiros termos … de uma sucessão definida por recorrência
🟢descobrir o termo geral de uma sucessão definida por recorrência [mais desafiante e não tão importante!]
🟢definir uma sucessão por recorrência, sabendo o termo geral [mais desafiante e não tão importante!]
Agora é a tua vez! 😁🔥Começa e pausa o vídeo para resolveres a alínea a) (a alínea b) é opcional) Quanto terminares, continua o vídeo para veres a resolução (qualquer dúvida, vê o exemplo anterior):
E agora pratica ainda mais! O exercício 2 (de descobrir o termo geral) é opcional – fá-lo como um desafio! 😉
📈Progressões Aritméticas e Geométricas
1. APRENDE A TEORIA
Quando nos queremos divertir a fazer sequências de números 😏, há duas maneiras óbvias: há o 1,2,3,4,5,… e há o 1,2,4,8,16,…
Na primeira, somamos sempre o mesmo valor, enquanto que na segunda multiplicamos sempre o mesmo valor. Assim, à primeira, chamamos de progressão aritmética e à segunda de progressão geométrica.
As progressões aritméticas e geométricas são os tipos mais sexy de sucessões. Como têm uma regra fácil para a sua criação, têm muitas propriedades jeitosas. 😁🔥
Vê o vídeo até aos 11.48 para aprenderes essas propriedades. É importante que percebas:
🔴 Como calcular o termo geral e a soma dos N primeiros termos destas progressões
2. APRENDE OS EXERCÍCIOS MAIS POPULARES
🔴 Tens o termo geral? Há 3 tipos de exercícios
Se já tens o termo geral, há 3 exercícios clássicos:
1. Calcular o termo de ordem N
2. Calcular a ordem do termo … (ou averiguar se o termo … pertence à sucessão)
3. Calcular a soma de N termos consecutivos (sejam eles os primeiros ou não)
Este vídeo aborda os dois primeiros exercícios para uma sucessão qualquer (nem precisa ser geométrica/aritmética):
O terceiro exercício (da soma de N termos consecutivos) é exclusivo às progressões aritméticas e geométricas, porque aqui tens de usar as respetivas fórmulas. Vê o vídeo (dos 22.40 ao fim):
🔴 Não tens o termo geral? Aprende a calculá-lo.
Há várias maneiras de calcular o termo geral. Mas há uma maneira que resulta sempre!
O enunciado dá-te sempre 2 equações diferentes:
1. Substitui todos os u_n nessas equações por u_1 e r (ou seja, pela fórmula do termo geral)
2. Resolve o sistema de equações (com variáveis u_1 e r)
3. Já sabes u_1 e r, por isso escreve o termo geral
O mais fácil é veres o exemplo (vê o exercício 6 todo):
⚠️NOTA: Nos exercícios em que te dão 2 termos da sucessão, não precisas de usar esta estratégia do sistema. Podes simplesmente escrever uma equação, como neste vídeo:
(mas atenção! É só mesmo neste caso! De resto, usa sempre a estratégia do sistema).
🔴 Estratégia Geral
Agora que já sabes os 3 exercícios clássicos e o termo geral, então os exercícios de progressões são sempre a mesma coisa:
1. Calcula o termo geral (resolve o sistema/equação)
2. Calcula o que a pergunta pedir (um dos 3 exercícios clássicos)
E não precisas de saber mais nada! 😁🔥 Se ainda não viste, vê este exemplo. E se já viste, vê outra vez!!!
Se reparares bem, os exercícios de progressões têm sempre as mesmas 4 frases:
1️⃣”A progressão é aritmética/geométrica”.
2️⃣ Primeira Equação
3️⃣ Segunda Equação
4️⃣ Pergunta (um dos 3 exercícios clássicos)
Agora que já percebeste, vamos praticar! (qualquer dúvida que tenhas, volta aos exemplos acima). Dos exercícios de exame seguintes, faz o 2, 3, 7, 14, 17 e 20:
3. APRENDE OS OUTROS EXERCÍCIOS
Há outros dois tipos de exercícios que ainda assim são bastante frequentes.
🔴”Averigua se/Mostra que é progressão aritmética/geométrica”
Imagina que já sabes o termo geral. Para mostrar que a progressão é
1️⃣ aritmética, mostra que a diferença entre o termo seguinte e o anterior é uma constante.
2️⃣ geométrica, então tens de mostrar que o quociente entre o termo seguinte e o anterior é uma constante.
Vê o exemplo abaixo no caso da progressão aritmética:
O caso da progressão geométrica segue a mesma lógica, só que tens de dividir o termo seguinte pelo anterior.
🔴”A soma de termos consecutivos é algo em termos de a e b. Determina esses a e b”
Aqui, o segredo é o mesmo no exercício anterior. Na progressão:
1️⃣ aritmética, a diferença entre o termo seguinte e o anterior é uma constante.
2️⃣ geométrica, o quociente entre o termo seguinte e o anterior é uma constante.
Com esta dica, faz agora os exercícios 11, 12, 15 e 19 (estes exercícios podem parecer mais difíceis, mas com calma chegas lá! 💪)
4. PRATICA AINDA MAIS! 😁🔥
🔴Mais Exercícios
| Ficha com todos os exercícios chave Prof. Mónica Pinto (website) | Ficha (com soluções) |
| Exercícios de Exame (faz o ex. 1 e 17) Prof. Paulo Correia (website) | Ficha Resolução |
🔴Faz tu: cria o teu próprio exercício!
Fala por experiência própria: nada mais surreal do que sentir que estamos a descobrir a matemática por nós próprios! Por isso, segue os passos seguintes e sente o poder da Matemática:
1️⃣Escreve o termo geral e os 10 primeiros termos da tua progressão aritmética/geométrica preferida (é com esta lista que vais verificar os teus resultados)
2️⃣Faz a pergunta que te apetecer:
🟢 Mostra que certo termo não pertence/não pertence à sucessão, calculando a sua ordem (escolhe termos que saibas que estarão ou não estarão na tua lista)
🟢 Calcula a soma dos termos consecutivos que estão na tua lista usando as fórmulas (depois verifica na tua calculadora somando todos esses termos)
🟢 Mostra que a tua progressão é aritmética e que não é geométrica (ou vice-versa)
Se quiseres criar exercícios mais complexos ainda, inspira-te na receita e nos exercícios que estão nos capítulos “Estratégia Geral” e A soma … Determina esses a e b”.
🔴Faz tu: esclarece dúvidas!
Falo por experiência própria: a melhor maneira de aprendermos é explicando aos outros. Junta-te ao meu servidor no Discord e poderás esclarecer as dúvidas de centenas de alunos! 😁🔥
🔴Desafio: Há alguma progressão que é ao mesmo tempo aritmética e geométrica?
Pensa e coloca a resposta abaixo nos comentários! 😁⬇️
🔬Propriedades das Sucessões
Vamos imaginar que somos matemáticos e que acabámos de inventar as sucessões. Agora, a grande pergunta é: quais são as características que tornam uma sucessão previsível e simpática?
Ou talvez seja mais fácil se pensarmos no seu gráfico: quais são os gráficos previsíveis e simpáticos?
😑Sucessões monótonas
O que é uma sucessão monótona?
Ora, um dos gráficos mais previsíveis simpáticos são aqueles em que os pontos estão sempre a subir↗️ou aqueles em que estão sempre a descer.↘️
Se está sempre a subir, então chamamos sucessão crescente. ↗️ Se está sempre a descer, então chamamos sucessão decrescente. ↘️
Mas agora nós queremos inventar outro nome: um nome que inclua todas estas sucessões, sejam elas crescentes ou decrescentes.
Ora, a todas as sucessões crescentes ou decrescentes, chamamos de sucessões monótonas. Monótonas porquê? Porque estar sempre a subir ou sempre a descer é um pouco seca. É um pouco monótono… 😏
Para reforçar o facto de que as sucessões crescentes ou decrescentes são mesmo monótonas, às vezes até as chamamos de sucessões monótonas crescentes ou monótonas decrescentes (mas a ideia é a mesma: sempre a subir ou sempre a descer).
E como é que chamamos as sucessões que não são monótonas? (ou seja, as que não são crescentes nem decrescentes?). Ora, é óbvio: são sucessões não monótonas. 😜
Agora que já demos nomes às nossas ideias, agora é só traduzir estes conceitos para Matemática! Vê as definições no vídeo:
🔴ATENÇÃO: Pela nossa definição, uma sucessão constante é, ao mesmo tempo, crescente e decrescente.
Exercícios – Estratégia Geral
Só com isto, já deves ser capaz de:
🔴 Mostrar que uma sucessão é (monótona) crescente
🔴 Mostrar que uma sucessão é (monótona) decrescente
🔴 Mostrar que uma sucessão não é crescente nem decrescente (ou seja, é não monótona)
A pergunta clássica é “Estude a sucessão quanto à monotonia”. Isto é só outra maneira de dizer: “diz-me se esta sucessão é crescente, se é decrescente ou se não nem é uma coisa nem outra (ou seja, não monótona)”.
Aqui a estratégia é sempre a mesma: calcular a diferença entre o termo seguinte e o termo anterior. E depois é veres o sinal dessa diferença:
🔴 Sempre positivo/zero: Crescente
🔴 Sempre negativo/zero: Decrescente
🔴 Às vezes positivo, outras negativo: Não monótona
Porém, nada melhor que um exemplo:
Como já deves ter percebido, para calcular e ver o sinal da diferença entre o termo seguinte e o anterior, precisas de saber bem trabalhar com frações e raízes.
🔴GRANDE LIÇÃO🔴
Quando vês monotonia, pensa logo na diferença entre o termo seguinte e o anterior
un+1 – un
Exercícios – fichas
| Exercícios Básicos e de Monotonia Mentes Brilhantes (website) | Ficha (com Soluções) |
Exercícios – faz tu!
EXERCÍCIO 1:
1.1 – Dá um exemplo do termo geral de uma progressão aritmética crescente e o de uma progressão aritmética decrescente.
1.2 – Mostra que essas progressões são de facto crescentes/decrescentes.
EXERCÍCIO 2:
2.1 – Dá um exemplo do termo geral de uma progressão geométrica crescente, o de uma progressão geométrica decrescente e o de uma progressão geométrica não monótona.
2.2 – Mostra que essas progressões são de facto crescentes/decrescentes/não monótonas.
EXERCÍCIO 3: Pega nas tuas sucessões preferidas e estuda-as quanto à monotonia (ou seja, diz se são não monótonas, monótonas crescentes ou monótonas decrescentes).
🔞Sucessões Limitadas
O que é uma sucessão limitada?
E agora, que outros gráficos de sucessões são também previsíveis e simpáticos?
Ora, são aqueles que estão sempre acima de um determinado valor. E queles que estão sempre abaixo de um determinado valor. No fundo, aquelas sucessões que têm um “chão” ou um “teto”.
A esse chão chamamos minorante (porque é menor/igual que todos). E a esse teto chamamos majorante (porque é maior/igual que todos).
Então, a uma sucessão com chão, ou seja, com minorante, chamamos de sucessão minorada. A uma sucessão com teto, ou seja, com majorante, chamamos de sucessão majorada.
E agora, aquelas sucessões que são ao mesmo tempo minoradas e majoradas? Ou seja, aquelas que têm ao mesmo tempo “chão” e “teto”? A essas, chamamos sucessões limitadas.
E se não for limitada, então é uma sucessão não limitada!
🔴ATENÇÃO: Se uma sucessão é não limitada, então é porque ou não tem teto ou não tem chão, isto é, ou não é majorada ou não é minorada.
🔴ATENÇÃO: os minorantes e os majorantes não são a mesma coisa que mínimo e máximo. O mínimo e o máximo são o menor e maior termos da nossa sucessão. Por outro lado, os minorantes e os majorantes, não precisam de ser termos da nossa sucessão (são apenas números menores/iguais ou maiores/iguais do que qualquer termo da nossa sucessão). Por exemplo, a sucessão 1/n tem minorante 0 mas não tem mínimo.
🔴ATENÇÃO: como os majorantes e minorantes não têm de ser termos da nossa sucessão, então se um majorante/minorante existir, este não é único. Por exemplo, 1/n tem minorante 0, -1, -1219, …. e majorante 1, 2, 725,…
Por isso, muitas vezes falamos no conjunto de minorantes e no conjunto de majorantes, para falarmos de todas as possibilidades de minorante/majorante. Por exemplo, 1/n tem conjunto de minorantes ]–∞,0] e conjunto de majorantes ]1,+∞[ (isto porque todos os termos de 1/n estão entre 0 e 1).
Agora que já demos nomes às nossas ideias, agora é só traduzir estes conceitos para Matemática! Vê as definições no vídeo (vê até aos 3:33):
Vê também este vídeo para perceberes graficamente as definições (vê até aos 23.16):
Exercícios – Estratégia Geral
Só com isto, já deves ser capaz de:
🔴 Identificar minorantes e majorantes de sucessões
🔴 Mostrar que uma sucessão é minorada, majorada, limitada ou não limitada
A pergunta clássica do “Verifica se é limitada” não é tão comum em exame, mas é bom que estejas confortável com ela. Esta tem estratégias diferentes dependendo da sucessão com que estás a trabalhar, mas a mais comum é quando o termo geral é uma fração:
ESTRATÉGIA MAIS COMUM (Frações)
1. Fazer divisão euclideana do numerador pelo denominador
2. Usar o facto de que “constante a dividir por não constante está sempre entre 0 e 1” para dar um minorante e um majorante à sucessão.
Mas nada mais fácil que ver o exemplo:
ESTRATÉGIA SECUNDÁRIA (quando a sucessão é às vezes negativa, outras vezes positiva)
Considera o módulo dessa sucessão e mostra que é sempre menor que um determinado valor (usando a estratégia atrás da divisão euclideana).
Se já souberes limites de sucessões, há uma outra maneira de mostrar que uma sucessão é limitada: é só calcular o limite (vê este capítulo).
Exercícios – fichas
| Exercícios de Sucessões Limitadas Mentes Brilhantes (website) | Ficha (com Soluções) |
| Exercícios de Sucessões Monótonas e Limitadas Prof. Érica Marques (website) | Ficha (com Soluções) |
Exercícios – faz tu!
EXERCÍCIO 1: Dá um exemplo do termo geral de uma sucessão:
1.1 – monótona e minorada
1.2 – monótona e majorada
1.3 – monótona e limitada
1.4 – monótona e não limitada
1.5 – não monótona e limitada (DICA: é uma progressão geométrica!)
EXERCÍCIO 2: Para cada uma das sucessões anteriores que sejam minoradas, majoradas ou limitadas, dá um exemplo de um minorante e/ou de um majorante.
EXERCÍCIO 3: Pega nas tuas sucessões minoradas, majoradas ou limitadas preferidas e mostra que são minoradas, majoradas ou limitadas.
🛣️Limites de Sucessões
Chega a uma altura da nossa investigação em que nós queremos descrever o que acontece no “fim” da sucessão.
É daqui que vem a ideia de limite. O limite da sucessão é o valor que está no “fim” da sucessão.
Agora o desafio será traduzir para linguagem matemática!
➡️Definição de limite convergente
Primeiro, inspiramo-nos em sucessões como 1/n.
Imagina o n a aumentar (podes imaginar o gráfico ou numericamente). Ora, vês que, à medida que o n aumenta, a sucessão embora nunca chegue a 0, está cada vez mais próxima de 0.
Neste caso, como está cada vez mais próxima de 0, dizemos que o limite é 0.
Num caso mais geral, quando o limite da sucessão é um número real qualquer, então nós dizemos que a sucessão é convergente (porque a sucessão converge para aquele número, ou seja, aproxima-se cada vez mais daquele número).
E agora, é traduzir esta definição para Matemática!
Não é muito importante saberes esta definição (porque não vais usá-la em mais lado nenhum). O mais importante mesmo é percebes a ideia intuitiva.
Mas se tiveres curiosidade, vê a definição neste vídeo:
🔀Limites divergentes
Mas claro, nem todas as sucessões são convergentes, ou seja, nem todas se aproximam de um número real.
A uma sucessão que não é convergente, nós chamamos de divergente. No fundo, “divergente” é o mesmo que “não convergente”, ou seja, que não se aproxima de nenhum número real.
🔴ATENÇÃO: Há duas maneiras principais de uma sucessão ser divergente:
1. A sucessão aproxima-se de um valor tão grande ou tão pequeno quanto quisermos porque nunca para de crescer/decrescer (o exemplo clássico é a sucessão n)
2. A sucessão nunca se aproxima de número nenhum porque está sempre a “saltar”. (o exemplo clássico é a sucessão (-1)n)
No segundo caso, como a sucessão não se aproxima de nada, então não há limite.
Porém, no primeiro caso, a sucessão de facto está-se a aproximar de alguma coisa – mas desta vez não é um número real, mas sim um valor tão grande ou tão pequeno quanto quisermos.
Neste caso, faz todo o sentido falarmos em limite, porque a sucessão aproxima-se de algo. Mas como não esse algo não é um número real, então não podemos usar a definição anterior – temos de criar outra definição de limite de propósito para estes casos.
↗️Definição de limite divergente para infinito
Consideremos então a sucessão n. Ora, à medida que o n aumenta, vês que a sucessão fica tão grande quanto quiseres.
Neste caso, nós dizemos que o limite é “mais infinito” e escrevemos lim n = +∞
🔴ATENÇÃO: “mais infinito” não é uma ideia mística nem misteriosa. É apenas um truque para facilitar a nossa comunicação (por exemplo, tu só tens um nome próprio que é para os outros chamarem por ti facilmente. Se não tivesses um nome, já viste o que seria? Como é que chamariam a tua atenção? “Ó tu! Ó tu aí!!! Sim, tu!!!” Pronto, já percebeste). A ideia com o “mais infinito” é a mesma: é só uma maneira fácil de dizer que é “um valor tão grande quanto quisermos”.
Do mesmo modo, consideramos a sucessão -n. Vemos que, à medida que o n aumenta, a sucessão fica tão pequena quanto quiseres.
Neste caso, nós dizemos que o limite é “menos infinito” e escrevemos lim n = –∞
Neste caso, “menos infinito” é só uma maneira fácil de dizer “um valor tão pequeno quanto quisermos”.
E agora, é traduzir esta definição para Matemática!
Mais uma vez, não é muito importante saberes esta definição (porque não vais usá-la em mais lado nenhum). O mais importante mesmo é percebes a ideia intuitiva.
Mas se tiveres curiosidade, vê a definição no vídeo:
🧮Como calcular limites
Da parte de limites, esta é a mais importante.
Limites imediatos
Primeiro, há muitas sucessões em que o limite é imediato. Além do limite da constante ser a própria constante, há outros limites também imediatos. Vê o vídeo até aos 1:02:12.
Álgebra de Limites
Agora que já sabemos os limites imediatos, podemos combiná-los usando a álgebra de limites. Vê o vídeo até aos 41:27:
Quando os limites são constantes, é óbvio. Mas como fazemos se tivermos infinitos?
Ora, os infinitos “engolem” tudo, mas os sinais importam. Percebe o que eu quero dizer com isto ao ver o vídeo até aos 56:30 (saltando a parte das demonstrações a meio):
🔴ATENÇÃO: Mais vocabulário (que não interessa mas que às vezes é utilizado):
Infinitamente grande positivo: sucessão com limite +∞
Infinitamente grande negativo: sucessão com limite –∞
Infinitésimo: sucessão com limite 0 (Dica: se 1/10 é um décimo e 1/100 é um centésimo, então 1/∞, ou seja, 0 é um infinitésimo! 😜)
Como levantar indeterminações
Como viste, há alturas em que a álgebra de limites não funciona.
Isto acontece quando um dos limites quer ser tão grande quanto quisermos enquanto quer ser tão pequeno quanto quisermos (+∞ vs –∞ no caso de +∞–∞ ou ∞ vs 1/∞ no caso de ∞/∞)
Para desempatar, temos então de ver qual é o limite mais rápido.
Sabendo o limite mais rápido, então podemos ignorar o mais lento (por exemplo, imaginando que é 0 ou uma constante) e já sabemos que o limite da sucessão será o limite do infinito mais rápido.
No fundo, a filosofia geral para resolver limites é:
“O termo mais rápido manda”
Por exemplo, intuitivamente, sabes logo que lim (n2–n) = lim n2 porque n2 é o termo mais rápido.
Porém, nós temos de ilustrar esta ideia matematicamente com aquilo que já sabemos. Para isso, temos de usar alguns truques, que dependem daquilo que estamos a trabalhar:
Polinómios (n…) ou exponenciais (…n): termo mais rápido em evidência
Raízes (√…): multiplicar pelo conjugado
Porém, nada mais fácil que ver em vídeo! Vê o vídeo até aos 16:05:
Estratégia Geral
Agora que já sabes todas as técnicas, é só pores em prática! Podemos combinar tudo o que já sabemos e criar uma estratégia geral! 😁🔥
ESTRATÉGIA GERAL
1. Substituir n por + ∞ (e ver se dá indeterminação)
2. Se dá indeterminação, usa um dos truques, corta alguns termos e substitui de novo o n por + ∞
Vê alguns exemplos neste vídeo:
Para uma outra perspetiva de como calcular os limites de sucessões, vê o meu vídeo de limites (até aos 26:51). Onde estiver x, imagina que está n – a estratégia é exatamente a mesma:
Exercícios: fichas
Está na hora de treinar! 😁🔥Onde disser “mostra o limite por definição”, substitui por “calcula o limite”:
| Exercícios de Limites de Sucessões: Prof. Mónica Pinto (website) | Ficha (com Soluções) |
| Exercícios de Limites de Sucessões 2: ex. 2 e 5 Prof. Mónica Pinto (website) | Ficha (com Soluções) |
Exercícios: faz tu!
EXERCÍCIO 1: Lembrando que a sucessão 1/n é uma sucessão não constante com limite 0, dá um exemplo de uma sucessão não constante:
1.1 – Com limite 2
1.2 – Com limite -3
1.3 – Crescente e com limite 0 (DICA: repara que 1/n é decrescente)
DICA: Pensa na álgebra de limites
EXERCÍCIO 2: Pega nas tuas sucessões preferidas com frações, raízes quadradas, potências, … (o que te apetecer!) e calcula o limite dessa sucessão (mas não inventes muito… 😂)
Depois, verifica a tua resposta na calculadora inteligente Wolfram Alpha (já deixei um exemplo no link – depois é só trocares pela sucessão que quiseres).
🔴ATENÇÃO: o WolframAlpha inicialmente faz limites de funções e não de sucessões (por isso, depois de cada pesquisa, deves ainda clicar em discrete para mudar para limites de sucessões):

🖇️Relação entre convergência, monotonia e limitação
Acabámos de definir três propriedades importantes de uma sucessão: monotonia, limitação e convergência.
E como qualquer matemático, após definirmos as propriedades importantes, nós queremos relacioná-las.
Investigando, vais ver que:
Convergente ⇒ Limitada (se é convergente, então é limitada)
Limitada + Monótona ⇒ Convergente (se é limitada e monótona, então é convergente)
Se queres perceber o porquê destas relações, vê o vídeo até aos 35:04:
Esquema-resumo
Porém, mesmo sabendo estas relações, não dá para perceber bem todas as possibilidades.
Nestas situações, os matemáticos têm um truque, que é organizar tudo num esquema (do género de diagrama de Venn):

Olhando para o esquema, vês que:
Convergente ⇒ Limitada (o mundo das sucessões convergentes vive dentro do mundo das sucessões limitadas)
Limitada + Monótona ⇒ Convergente (quando os mundos das sucessões limitadas e das sucessões monótonas se intersetam, estamos obrigatoriamente no mundo das funções convergentes)
Uma sucessão pode ser convergente mas não monótona (o mundo das sucessões convergentes não está todo dentro do mundo das sucessões monótonas)
Mas tudo se torna mais fácil de lembrar quando dás um exemplo clássico a cada sucessão:
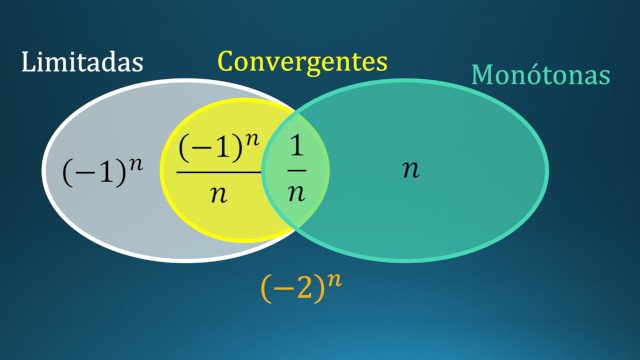
Aqui, (-2)n é um exemplo de uma sucessão que ao mesmo tempo não é limitada (porque a sucessão fica tão grande e tão pequena quanto queremos) e não é monótona (porque está sempre a saltar).
De facto, combinando as três sucessões clássicas: 1/n, n e (-1)n (uma que é convergente, outra divergente para +∞ e outra divergente sem limite), consegues criar uma sucessão com as propriedades que te apetecerem! (claro, pode ser preciso adicionar/multiplicar constantes 😉)
CURIOSIDADE: repara que Monótona ⇒ tem limite, ou seja, todas as sucessões monótonas têm limite (seja ele um número real ou ±∞). Isto porque se uma sucessão é monótona então temos duas opções:
1️⃣é também limitada e então é convergente (ou seja, o limite é um número real)
2️⃣não é limitada e então será divergente para ±∞ (ou seja, o limite é ±∞).
Exercícios – faz tu!
EXERCÍCIO 1: Dá um exemplo de uma sucessão:
1.1 – monótona e divergente
1.2 – monótona e convergente
1.3 – não monótona e divergente
1.4 – não monótona e convergente
1.5 – monótona e limitada
1.6 – não monótona e limitada
1.7 – monótona e não limitada
1.8 – não monótona e não limitada
1.9 – decrescente e limitada
1.10 – crescente e limitada
1.11 – crescente e convergente
1.12 – crescente e divergente
DICA: Inspira-te nos exemplos clássicos acima 😏
EXERCÍCIO 2: Dá um exemplo de uma sucessão:
2.1 – Monótona e convergente para 1.
2.2 – Crescente e convergente para -2
2.3 – Não monótona e convergente para 1.
DICA: combina os exemplos clássicos acima
EXERCÍCIO 3: Dá um exemplo de uma sucessão:
2.3 – Não monótona e divergente para +∞
2.4 – Não monótona e divergente para – ∞.
DICA: um exemplo é …2 (descobre esse “…”)
Mostrar que uma sucessão é limitada (2ª maneira)
Já vimos que Convergente ⇒ Limitada. Isto significa que há uma 2ª maneira de demonstrar que uma sucessão é limitada!
Mostrar que sucessão é limitada
[2ª Maneira]:
Calcula o limite da sucessão
(se for um número real, já sabes que a sucessão é convergente, logo é limitada!)
🔴ATENÇÃO: Se a sucessão não tiver limite, isso não significa que não seja limitada (lembra-te do exemplo clássico (-1)n).
🔴ATENÇÃO: Esta estratégia só é útil para mostrar que uma sucessão é limitada – ela não te diz nada sobre os minorantes e majorantes.
Descobrir minorantes e majorantes usando monotonia e convergência
Mas se pensarmos bem, tanto a monotonia como a convergência dão-nos pistas sobre os minorantes e majorantes.
Se pensares no gráfico de uma sucessão, chegas rapidamente à conclusão de que:
🟢Se é crescente, então o 1º termo é um minorante
🟢Se é decrescente, então o 1º termo é um majorante.
E agora, imagina que sabemos que essa sucessão é também convergente e pensa no gráfico. Rapidamente percebes que:
🟢 Se é crescente e convergente, então o 1º termo é um minorante e o limite é um majorante
🟢Se é decrescente e convergente, então o 1º termo é um majorante e o limite é um minorante.
Nenhuma destas conclusões é extraordinária – é só imaginares o gráfico. Ou então podes pensar:
🟢Se uma sucessão cresce sempre, então o primeiro termo é o menor e o “último” termo (o limite) é o maior.
🟢Pelo contrário, se decresce sempre, então o primeiro termo é o maior e o “último” termo (o limite) é o menor.
🤫Outras Dicas e Truques
Maneiras de visualizar uma sucessão
Para entender uma sucessão, há várias coisas que podes fazer:
- Calcular os primeiros termos e escrevê-los em sequência (por exemplo, 1,3,5,7,…)
- Calcular os primeiros termos e desenhar o gráfico
- Esboçar todo o gráfico como se fosse uma função (quando sabes limites, monotonia ou limitação)
- Definir a sucessão por ramos (principalmente quando tens (-1)n, (-2)n e companhia, separando os casos em que n é par e em que n é ímpar)
Lidar com (-1)n e companhia
Para lidar com as sucessões que têm (-1)n, (-2)n, etc, há duas opções:
- definir a sucessão por ramos (é o que fazes na maioria das vezes, em que separas o caso em que n é par e em que n é ímpar)
- considerar o módulo dessa sucessão (fazes principalmente para ver se a sucessão é limitada)
Descobrir termos de ordem par/ímpar
Quando pedem por termos de ordem par ou ímpar, basta lembrares que:
Números pares: números da forma 2k
Números ímpares: números da forma 2k-1
(em que k é um número inteiro)
Mas se estivermos a falar de ordens (que são números naturais 1,2,3…), então:
Ordens pares: números da forma 2k
Ordens ímpares: números da forma 2k-1
(em que k é um número natural)
Depois, para resolver o exercício, é só substituíres o teu n por 2k ou 2k-1. Vê, por exemplo, o exercício 1 seguinte:
Soma de termos consecutivos de uma progressão que não começa no primeiro
Tu já sabes fazer a soma dos N primeiros termos – é só usares a fórmula.
Mas e se a soma não começar no primeiro termo? Por exemplo:
QUESTÃO: Seja un=2n. Calcula a soma
u4 + u5 + u6
Fazendo à mão, vias rapidamente que o resultado é 30 (mas como é óbvio, fazer à mão não funciona muito bem se estiveres a somar 100 termos).
Aqui, há duas maneiras de resolver (e nenhuma delas é fazer a conta à mão😜).
A primeira maneira é a seguinte:
No fundo:
PRIMEIRA MANEIRA
Soma todos os termos até ao último (fórmula) e subtrai a soma dos primeiros termos que não interessam (fórmula)
Esta é a maneira mais simples de perceber.
EXERCÍCIO 1: Mostra que o resultado é 30 por esta primeira maneira.
Mas há outra maneira mais rápida: podes aplicar a soma dos N primeiros não a esta sucessão, mas sim à sucessão em que começas logo no termo que te interessa (ignorando os primeiros termos que não te interessam)
Neste caso, como queres saber o u4 + u5 + u6, então começas a tua nova sucessão no u4 (ignorando os termos u1, u2, u3, que não interessam).
Primeiro, se queres aplicar a soma dos N primeiros termos, então tens de saber o N, ou seja, o número de termos dessa soma.
Neste caso, é fácil. Mas no caso geral, qual é o truque? O truque é pensar como há pouco: ao número de todos os termos até ao último (neste caso, 6) subtrais o número dos primeiros termos que não interessam (neste caso, 3). Ficas então com N=6-3=3 termos, como previsto.
🔴ATENÇÃO: No caso geral, a tua tentação seria fazer último – primeiro, ou seja, 6-4 (o que dava errado). A maneira fácil de pensares é todos – não interessa, ou seja, 6-3.
Agora que sabes o número de termos da tua soma N, é só aplicares a fórmula. Repara que esta nova sucessão tem a mesma razão que a original, só que agora o primeiro termo é u4 (e, na progressão aritmética, o último termo será u4+r(N-1) pela fórmula do termo geral).
Resumindo:
SEGUNDA MANEIRA
1. Calcula o número de termos N da tua soma (todos – não interessam)
2. Aplica a fórmula da soma (mesma razão, diferente primeiro termo)
EXERCÍCIO 2: Mostra que o resultado é 30 por esta segunda maneira.
EXERCÍCIO 3: Faz o mesmo exercício só que para uma progressão geométrica à tua escolha.
🌍Fichas Globais
Testa todos os teus conhecimentos de Sucessões 11º Ano com estes exercícios – tem de tudo um pouco! 😁🔥
| Propriedades, Progressões e Limites (faz todos menos o 17) Prof. Alexandre Areias (website) | Ficha Resolução |
| Propriedades, Progressões e Limites Prof. Érica Marques (website) | Ficha (com soluções) |
| Exercícios Desafiantes José Carlos Pereira (website) | Ficha (com resoluções em vídeo) |
⏱️Testes-modelo
Não há melhor preparação para testes do que fazer testes-modelo cronometrados.
Se em aula nunca fizeste exercícios de demonstrar limites por definição, então onde disser “mostra o limite por definição”, substitui por “calcula o limite”.
🤝Preciso da tua ajuda!
Envia-me para geral@ricardo-ferreira.pt soluções ou resoluções destas fichas (de preferência, escritas a computador).
1. Generalidades sobre Sucessões
2. Sucessões por Recorrência
3. Qualquer outra ficha que só tenha soluções mas não resoluções
Envia-me também para geral@ricardo-ferreira.pt qualquer teste ou ficha de avaliação sobre Sucessões 11º Ano (que já seja do tempo das Aprendizagens Essenciais).
Se quiseres, coloca também o teu nome/website nas resoluções. Muito obrigado pela ajuda! 😁❤️
🚉Próxima Paragem!
- Limites de Funções 11º Ano (a dada altura… 😜)
Até lá, recebe todas as novidades por email subscrevendo na Newsletter abaixo 😁⬇️





